Have you ever found your team or group in a situation where you had to make a complex decision? Maybe you came to an impasse, unable to decide between two or more options, or maybe you selected one and still doubted whether you had evaluated all possible pros and cons. Well, what if I told you that there's a way to easily use a little math and psychology to organize and rank your options to determine the best solution?
What if I further told you that these techniques can be applied to a wide variety of decisions, like selecting which framework you should use to create your new application, or even deciding which dog you should adopt?

Decision Theory
Decision theory is the study of decisions and their consequences. The subject is not a very unified one. There are many different ways to theorize about decisions, and therefore there are also many different research traditions.
Modern decision theory has developed since the middle of the 20th century through contributions from several academic disciplines. Although it is now clearly an academic subject in its own right, decision theory is typically pursued by researchers who identify themselves as economists, statisticians, psychologists, political and social scientists, or philosophers.
There is some division of labor among these disciplines. For instance, a political scientist is likely to study voting rules and other aspects of collective decision-making, a psychologist the behavior of individuals making decisions, and a philosopher the requirements for rationality in decisions.
When looking into how organizations usually make decisions, we notice a constant desire to have clear, objective, and mathematical criteria. However, decision making is, in its totality, a cognitive and mental process of selecting one out of the highest possible number of adequate options based on tangible and intangible criteria, and these criteria do not even necessarily have to be justified by the decision makers.
There are various ways of dividing the decision making process, but to simplify, we can split it into 5 basic steps:
- Defining the problem
- Listing the possible solutions
- Identifying the criteria and outcomes implied in each solution
- Selecting and applying one MCDM Method (Multiple-Criteria Decision-Making Method)
- Making your decision based on the rank of solutions
Multi-Criteria Decision-Making Methods
Multi-Criteria Decision-Making Methods provide ways for us to evaluate the multiple, often conflicting criteria involved in decision making. It's typical to have conflicting criteria when evaluating options, e.g. in an aggregated value decision, where cost considerations are often in conflict with quality considerations.
There are plenty of known MCDM Methods. Let's look at some of the most popular: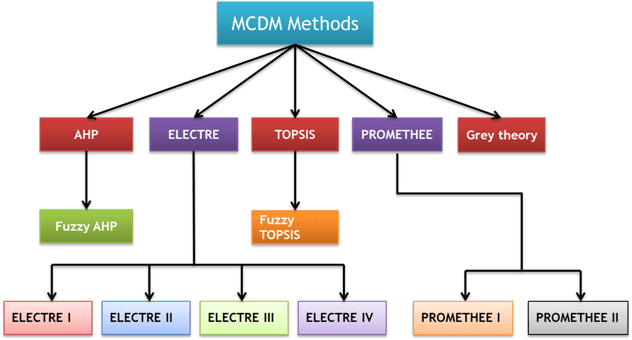
Image courtesy of researchgate
ELECTRE (ELimination Et Choix Traduisant la REalite) and PROMETHEE (Preference Ranking Organization METHod for Enrichment of Evaluations) are the main methods used in the French family of theory decision studies. These methods allow decision makers to select the best choice with the biggest advantage and the least conflict between various criteria. Different versions of both methods have been developed, but all methods are based on the same fundamental concepts; they just differ operationally and according to the type of decision being made. The main idea is the proper utilization of “outranking relations.” They enable decision makers to model a decision process by using coordination indices. These indices are concordance and discordance matrices. The decision maker uses concordance and discordance indices to analyze outranking relations among different alternatives and to choose the best alternative using CRISP data.
Grey Theory's decision making techniques are highly mathematical. This MCDM Method is based on fuzzy logic and is used to address problems whose variables are partly known and partly unknown, being defined as "insufficient data" and "weak knowledge." The idea is to have a large amount of input data and to examine it in an interactional manner.
TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) is a method of compensatory aggregation that compares a set of alternatives by identifying weights for each criterion, normalizing scores for each criterion, and calculating the geometric distance between each alternative and the ideal solution, which is the best score in each criterion. An assumption of TOPSIS is that the criteria are monotonically increasing or decreasing.
Finally, we have AHP, one of the most widely used MCDM Methods. We'll focus on AHP today since it's mathematically simple compared to the other methods listed above and since it allows us to compare criteria without previously assigning numeric metrics to them. Here's how AHP can be used to easily make a complex decision.
The AHP MCDM Method
Developed by Thomas L. Saaty in the 1970s, AHP, or Analytic Hierarchy Process, is a technique for group decision making wherein the problem is decomposed into a hierarchy of more easily comprehensible sub-problems, each of which can be analyzed independently.
Once the hierarchy is built, the decision makers evaluate various alternatives by comparing them to each other two at a time. In making the comparisons, the decision makers can use concrete data about the elements, but they typically use their own judgments about the elements' relative meaning and importance. In fact, the premise that human judgments can be used in performing evaluations is essential to the AHP.
The AHP then converts these evaluations into numerical values that can be processed and compared over the entire range of the problem. A numerical weight is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way.
In the final step of the process, numerical priorities are calculated for each of the decision alternatives. These numbers represent each alternative's relative ability to achieve the decision goal and voila, you have your rational decision!
A Practical Example
Let's go through a simple, existent example published on Wikipedia to understand how the AHP really works. Imagine that we need to select a new CEO for a traditional, big company. The board of directors has selected three possible candidates (Tom, Dick and Harry), but they are struggling to decide who will be the new CEO since some BOD members aren't sure which skills should be prioritized in this process.

According to the AHP, the first step is to define a hierarchy of sub-criteria that we can use to compare the options. In this case, the board decided that the four main criteria should be: Experience, Education, Charisma, and Age.

Having defined the criteria, we now need to start comparing the options pairwise. In order to do that, we are going to create a WCM, Weight Comparison Matrix, for each criterion. This will measure the relative degree to which each option of the pair accomplishes this specific criterion. The WCM is a square NxN matrix, where N is the number of options that we have, in this case 3. The values of this matrix should be filled by comparing the column number option with the line number option in the given criterion, and these values should be defined using the fundamental scale for pairwise comparisons.

After filling the matrix, we sum the values in the line for a given option and divide it by the sum of the values of the whole matrix, defining a priority for this given option relative to this specific criterion. There are a few online calculators that can do this for us after we define the pairwise comparison values. These calculators usually provide an inconsistency factor based on the filled values, indicating how inconsistent the comparison structure of the matrix is based on the fundamental scale for pairwise comparisons. The following images break down each stage of this process:

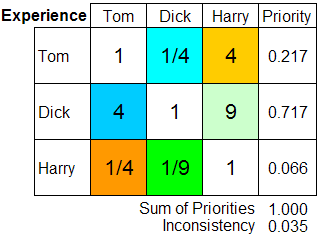






After defining the WCM of each option for each criterion, we now need to calculate the importance between the criteria themselves. We are going to use the same pairwise comparison method, but using a CxC WCM, where C is the number of criteria.


Now for our final step, we are going to calculate the criterion weight by multiplying each criterion priority by the corresponding option priority. Then, we sum all the weighted criteria by option, having a final score for each option over the main goal.

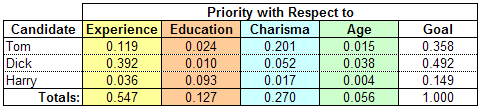
Based on the board's choice of decision criteria and their judgment about the relative importance of each one, Dick, with a priority of 0.492, is by far the most suitable candidate. Tom, with a priority of 0.358, is second, and Harry, at 0.149, is third.
Benefits of Using AHP
Not only do our board members now have a logical decision, but also, because they have used the AHP, it is easy for them to trace their thinking and to justify the steps that led to their decision. If they have second thoughts about the final outcome, they can revisit the process and make changes if needed. They can also, if they deem it helpful, reveal the details of their process to their consultants, candidates, stakeholders, or to anyone else who might be concerned with the decision.
So next time you and your team aren't sure which option will best accomplish its goal, give the Analytic Hierarchy Process a try!
Author
Fábio Suarez
Fábio Suarez is a Java Engineer at Avenue Code who works with microservices applications.





